obryanjf
Recycles dryer sheets
My take on the 6% Guyton SWR. It does not exist without some serious risk in purchasing power. The 6% SWR paper was on a previous thread a week or 2 ago.
My model and its flaws to get the dirty laundry out; not the same data as Guyton’s, I use Gummy’s, I do not have a monte carlo simulator, I use rolling 40 year periods from 1928 to 2000, when rolls out of 2000 it rolls into 1928 again. This yields 75 periods, and this is similar to FIRECALC except the rolling out piece. I have coded 4 equity asset classes rather then 8, due to not having lots of asset class data and not caring to invest the hour or so to code it. Everything else is my interpretation of Guyton’s description and I believe close to what he intended. The 8 asset classes likely improve the DR model a bit, but I believe not materially.
DYODD: I’m an engineer with a MBA, but not a statistian nor a programmer, just a hack. Take the data with a grain of salt and hopefully someone else will evaluate and confirm. I believe it is pretty close.
The issue I have with the original Guyton model is the lost purchasing power (PP). He tries to evaluate this by calculating a final PP (inflation adjusted; IA) and the sum of all withdrawls (IA).
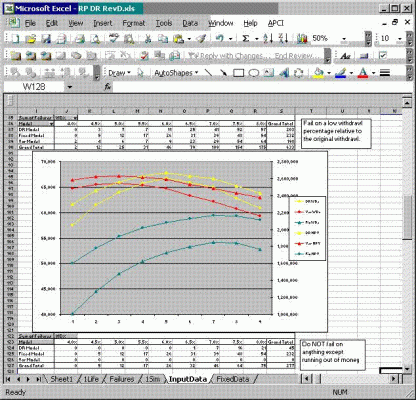
Let me explain the graph. My runs are a 10,20,40,10,10,10,10 (cash, fixed, s&p, small value, large value, small growth) or 10 cash, 20 fixed, 70 equity. No great reason, just my last data check. Now there is a small table on the top and bottom of the graph. The bottom is the total failures for the original Guyton methodology (2006 paper) extended to include his model (DR Model), using the Fixed at retirement model (FIRECALC) and a pure play variable model (x % of previous year net worth).
I think the bottom results are inline with what I would expect. The run is from a withdrawl % (WD%) from 4% to 8% in 0.5% increments. Var model never fails, DR model fails at high WD % because it cannot react fast enough sometimes and fixed is inline with other calculators. Now the top table details when I toggle on failures if the IA withdrawls on a year are less than 50% of the initial withdrawl. Once it fails, that run is a failure, but the run continues, so the end data (averages, etc) would be the same either way. Note if a run fails, the withdrawls sometimes pick up to greater then 50%, but I think 50% is a point I do not what to go during ER. This failure scenerio is one I think Guyton should focus more on.
Note the fixed model runs at a constant IA withdrawl and runs to extinction if foretold by the numbers. The var model and DR model run pretty similar, but ultimately the DR model has more failures at higher WD%.
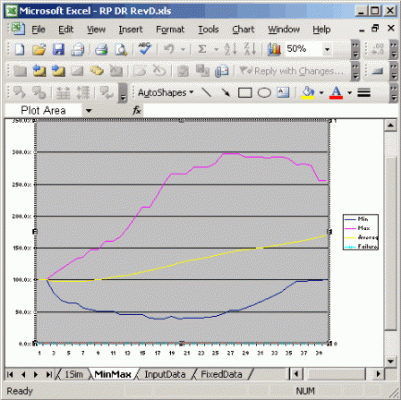
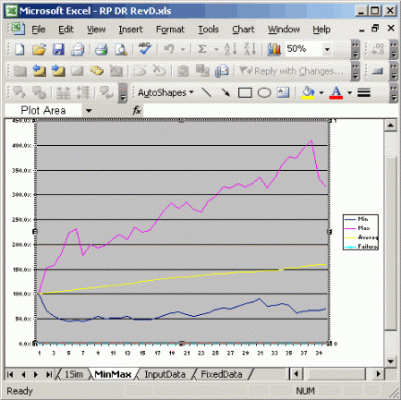
The graph shows the NPV(sum of all IA withdrawls over a run) and the IA withdrawls averaged. Note the var model works better at lower WD% (4% to 5%) and the DR model at higher WD% (5% to 8%)
In conclusion: I think the var model provides a better and simpler model for a variable PP withdrawl strategy. Just looking at the end IA WD and the NPV IA WD’s does not do justice to understanding what happens from year 1 to year 40. A failure triggering on <50% (or similar) is key to being able to compare different models. There may be a DR model out there that keeps the PP above some bottom and does not run to extintion, but I do not think this is it.
What will I do? Hope a better DR model emerges by the time I get to critical mass and if not, probably WD about 5% using a var model or a simplier DR model.
Comments?
job
BTW the 64k limit is a pain, that is why the picture is a bit flaky.
My model and its flaws to get the dirty laundry out; not the same data as Guyton’s, I use Gummy’s, I do not have a monte carlo simulator, I use rolling 40 year periods from 1928 to 2000, when rolls out of 2000 it rolls into 1928 again. This yields 75 periods, and this is similar to FIRECALC except the rolling out piece. I have coded 4 equity asset classes rather then 8, due to not having lots of asset class data and not caring to invest the hour or so to code it. Everything else is my interpretation of Guyton’s description and I believe close to what he intended. The 8 asset classes likely improve the DR model a bit, but I believe not materially.
DYODD: I’m an engineer with a MBA, but not a statistian nor a programmer, just a hack. Take the data with a grain of salt and hopefully someone else will evaluate and confirm. I believe it is pretty close.
The issue I have with the original Guyton model is the lost purchasing power (PP). He tries to evaluate this by calculating a final PP (inflation adjusted; IA) and the sum of all withdrawls (IA).
Let me explain the graph. My runs are a 10,20,40,10,10,10,10 (cash, fixed, s&p, small value, large value, small growth) or 10 cash, 20 fixed, 70 equity. No great reason, just my last data check. Now there is a small table on the top and bottom of the graph. The bottom is the total failures for the original Guyton methodology (2006 paper) extended to include his model (DR Model), using the Fixed at retirement model (FIRECALC) and a pure play variable model (x % of previous year net worth).
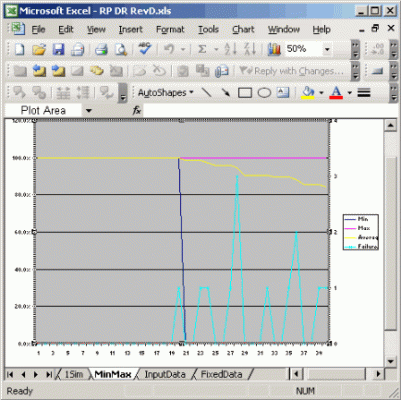
I think the bottom results are inline with what I would expect. The run is from a withdrawl % (WD%) from 4% to 8% in 0.5% increments. Var model never fails, DR model fails at high WD % because it cannot react fast enough sometimes and fixed is inline with other calculators. Now the top table details when I toggle on failures if the IA withdrawls on a year are less than 50% of the initial withdrawl. Once it fails, that run is a failure, but the run continues, so the end data (averages, etc) would be the same either way. Note if a run fails, the withdrawls sometimes pick up to greater then 50%, but I think 50% is a point I do not what to go during ER. This failure scenerio is one I think Guyton should focus more on.
Note the fixed model runs at a constant IA withdrawl and runs to extinction if foretold by the numbers. The var model and DR model run pretty similar, but ultimately the DR model has more failures at higher WD%.
The graph shows the NPV(sum of all IA withdrawls over a run) and the IA withdrawls averaged. Note the var model works better at lower WD% (4% to 5%) and the DR model at higher WD% (5% to 8%)
In conclusion: I think the var model provides a better and simpler model for a variable PP withdrawl strategy. Just looking at the end IA WD and the NPV IA WD’s does not do justice to understanding what happens from year 1 to year 40. A failure triggering on <50% (or similar) is key to being able to compare different models. There may be a DR model out there that keeps the PP above some bottom and does not run to extintion, but I do not think this is it.
What will I do? Hope a better DR model emerges by the time I get to critical mass and if not, probably WD about 5% using a var model or a simplier DR model.
Comments?
job
BTW the 64k limit is a pain, that is why the picture is a bit flaky.